|
Subiectul I
1. Să se ordoneze crescător numerele  . .
Rezolvare: Pentru a compara numerele date, le vom scrie astfel:
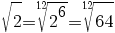 ; ;
 ; ;
 . .
Avem

sau
 . .
2. Să se determine valoarea minimă a funcţiei 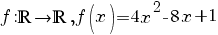 . .
Rezolvare: Valoarea minimă a funcţiei f este
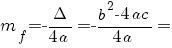
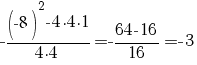 . .
Deci, 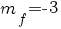 . .
3. Să se rezolve în mulţimea numerelor reale ecuaţia 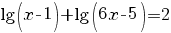 . .
Rezolvare: Punem condiţiile de existenţă a logaritmilor:

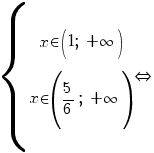
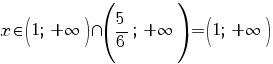 . .
Prin urmare, domeniul de existenţă a soluţiilor ecuaţiei este 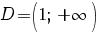 . .
Atunci
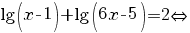


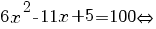
 . .
Avem


şi
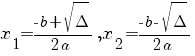
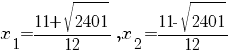

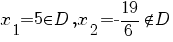 . .
Prin urmare, soluţia ecuaţiei date este  . .
4. Să se determine probabilitatea ca, alegând un număr din mulţimea numerelor naturale de două cifre, acesta să fie pătrat perfect.
Rezolvare: Să notăm cu A evenimentul
A: Alegând un număr din mulţimea numerelor naturale de două cifre, numărul ales este pătrat perfect.
Atunci
 . .
Există 6 pătrate perfecte de două cifre: 16; 25; 36; 49; 64 şi 81. Avem  de cazuri posibile (câte numere naturale de două cifre sunt). Prin urmare de cazuri posibile (câte numere naturale de două cifre sunt). Prin urmare
 . .
5. Să se determine ecuaţia dreptei care trece prin punctul 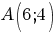 şi este perpendiculară pe dreapta şi este perpendiculară pe dreapta  . .
Rezolvare: Ecuaţia dreptei d este echivalentă cu
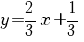 . .
Prin urmare, panta dreptei d este
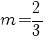 . .
Panta m’ a dreptei d’ care trece prin punctul A şi este perpendiculară pe dreapta d verifică relaţia
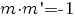
şi prin urmare este
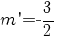 . .
Ecuaţia dreptei d’ este atunci
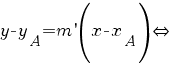
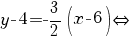

 . .
Deci, dreapta d’ care trece prin punctul A şi este perpendiculară pe dreapta d este
 . .
6. Ştiind că 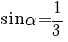 , să se calculeze , să se calculeze  . .
Rezolvare: 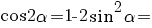
 . .
Subiectul II
1. Se consideră matricea 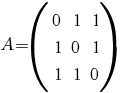 . .
a) Să se verifice egalitatea  . .
b) Să se calculeze 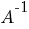 . .
c) Să se arate că 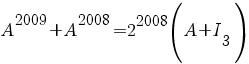 . .
Rezolvare:
a) Avem:

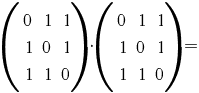
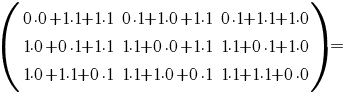
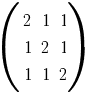 . .
Atunci
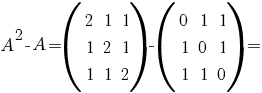
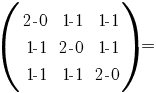

 , c.c.t.d. , c.c.t.d.
b) La pct. a) s-a demonstrat că
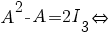
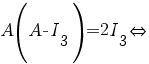
![A[1/2 (A-I_{3})]=I_{3} A[1/2 (A-I_{3})]=I_{3}](/~spt/plugins/content/mathpublisher/img/math_971_27c4faf4f1f52b95d5d5fb6f214911fd.png) . .
Analog rezultă şi relaţia
![[1/2 (A-I_{3})]A=I_{3} [1/2 (A-I_{3})]A=I_{3}](/~spt/plugins/content/mathpublisher/img/math_971_55596d423db5a5b0033831b5ef4f373e.png) . .
Prin urmare


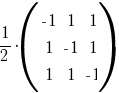 . .
c) Vom demonstra că pentru orice număr natural nenul n, are loc
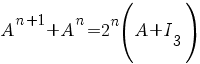 . .
Fie predicatul unar P, dat de  . .
Vom demonstra prin inducţie matematică după n că P(n) este o propoziţie adevărată oricare ar fi n număr natural nenul.
I. 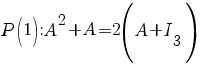 . .
Conform pct. a), avem


 . .
Aşadar, propoziţia P(1) este adevărată.
II. 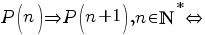
 . .
Ştim că
 ; ;
înmulţind la stânga ambii membri ai acestei egalităţi cu A, obţinem
![A(A^{n+1}+A^{n})=A[2^{n}(A+I_{3})]{doubleleftright} A(A^{n+1}+A^{n})=A[2^{n}(A+I_{3})]{doubleleftright}](/~spt/plugins/content/mathpublisher/img/math_971_54649a707f75d0d35d8ef8e2aa679574.png)
![A(A^{n+1}+A^{n})=2^{n}[A(A+I_{3})]{doubleleftright} A(A^{n+1}+A^{n})=2^{n}[A(A+I_{3})]{doubleleftright}](/~spt/plugins/content/mathpublisher/img/math_971_c07e2037714a6c5dd6086d31f4826f00.png)
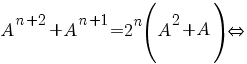 (dacă ne folosim de pasul I) (dacă ne folosim de pasul I)
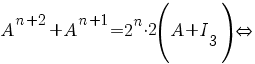
 . .
Prin urmare, 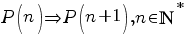 . .
Din I şi II, aplicând principiul inducţiei matematice, rezultă că propoziţia P(n) este adevărată pentru orice număr natural nenul, adică
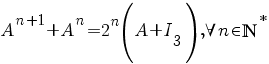 , ,
de unde pentru n=2008 se obţine egalitatea care trebuia demonstrată:
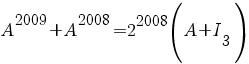 . .
2. Se consideră că 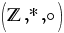 este un inel comutativ, unde este un inel comutativ, unde
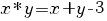
şi
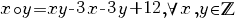 . .
a) Să se arate că elementul neutru al legii de compoziţie ‘ ’ este 4. ’ este 4.
b) Să se determine  astfel încât între inelele astfel încât între inelele 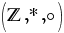 şi şi  să existe un izomorfism de forma să existe un izomorfism de forma  . .
c) Să se rezolve în mulţimea  ecuaţia ecuaţia  . .
Rezolvare: a) Numărul  este element neutru al legii de compoziţie ‘ este element neutru al legii de compoziţie ‘ ’ dacă şi numai dacă ’ dacă şi numai dacă


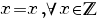 , (A). , (A).
Deci, numărul întreg 4 este element neutru pentru legea de compoziţie ‘ ’. ’.
b) Funcţia  este un izomorfism între inelele este un izomorfism între inelele 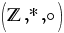 şi şi  dacă şi numai dacă: dacă şi numai dacă:
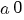 (adică f este bijectivă) (adică f este bijectivă)
şi
 . .
Atunci

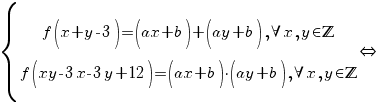
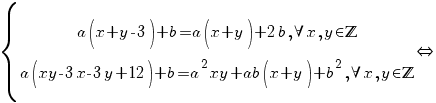
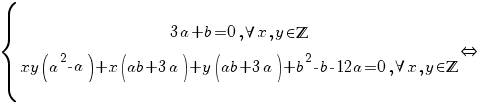
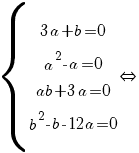
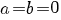 sau sau  . .
Dar cum 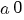 , rezultă că pentru , rezultă că pentru 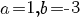 există un izomorfism între cele două inele, dat de legea există un izomorfism între cele două inele, dat de legea 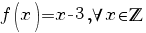 . .
c) Ecuaţia
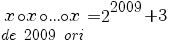
este echivalentă, dacă ţinem seama că f este un izomorfism de inele, cu:


![[f(x)]^{2009}=2^{2009}+3-3{doubleleftright} [f(x)]^{2009}=2^{2009}+3-3{doubleleftright}](/~spt/plugins/content/mathpublisher/img/math_980_600d33f3401f270c4deb85807583cca2.png)
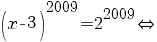
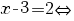
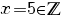 . .
Subiectul III
1. Se consideră funcţia 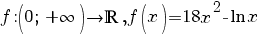 . .
a) Să se determine intervalele de monotonie ale funcţiei f.
b) Să se determine  pentru care pentru care 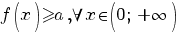 . .
c) Să se determine numărul de rădăcini reale ale ecuaţiei 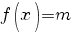 , unde m este un parametru real. , unde m este un parametru real.
Rezolvare:
a) Funcţia f este derivabilă pe  şi şi
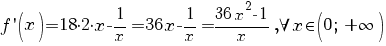 . .
Avem
I. 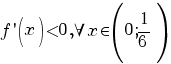 ; ;
II. 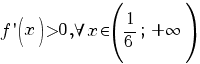 ; ;
III. 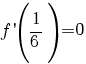 . .
Prin urmare, funcţia f este strict descrescătoare pe intervalul 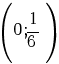 şi strict crescătoare pe intervalul şi strict crescătoare pe intervalul 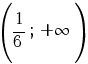 . .
b) În plus, avem:
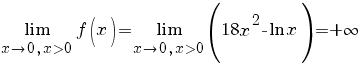 ; ;
iar
(*) 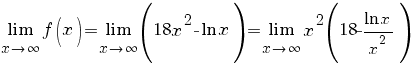 . .
Aplicând teorema lui l’Hopital, obţinem:
 . .
Cu aceasta, revenind la calculul limitei (*), obţinem
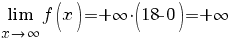 . .
Rezumând cele de mai sus, rezultă că
 . .
Întrucât
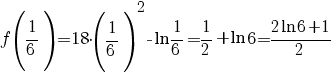
rezultă că pentru orice 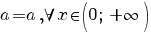 . .
Deci, ![a in ({-infty}; ~ {2 ln {6}+1}/2] a in ({-infty}; ~ {2 ln {6}+1}/2]](/~spt/plugins/content/mathpublisher/img/math_992.5_b4c1998b2219348fdeb54da11a868a73.png) . .
Tabloul de variaţie al funcţiei f este:

c) Analizând tabloul de variaţie al funcţiei f, rezultă că:
I. Pentru 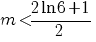 ecuaţia ecuaţia 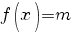 nu are soluţii reale; nu are soluţii reale;
II. Pentru 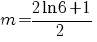 ecuaţia ecuaţia 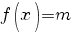 are o soluţie dublă, pe are o soluţie dublă, pe  ; ;
III. Pentru  ecuaţia ecuaţia 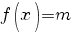 are două soluţii reale. are două soluţii reale.
2. Se consideră funcţiile 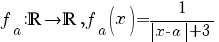 , unde , unde  . .
a) Să se arate că pentru orice  , funcţia , funcţia 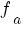 are primitive strict crescătoare pe are primitive strict crescătoare pe 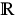 . .
b) Să se calculeze 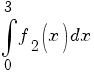 . .
c) Să se calculeze 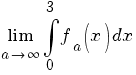 . .
Rezolvare:
a) Pentru orice  , funcţia , funcţia 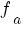 este continuă pe este continuă pe 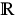 , ca funcţie care se obţine în urma unor operaţii cu funcţii elementare, cum ar fi compunerea, adunarea sau raportul a două funcţii. Prin urmare, această funcţie admite primitive pe , ca funcţie care se obţine în urma unor operaţii cu funcţii elementare, cum ar fi compunerea, adunarea sau raportul a două funcţii. Prin urmare, această funcţie admite primitive pe 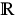 . Întrucât funcţia . Întrucât funcţia 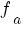 este strict pozitivă pe este strict pozitivă pe 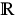 , toate primitivele acestei funcţii sunt strict crescătoare pe , toate primitivele acestei funcţii sunt strict crescătoare pe 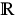 . .
b) Avem:
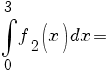
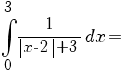
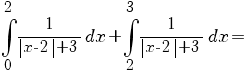


![=[- ln {(-x+5)}] delim{|}{{{~}under{0}}over{2}}{} + [ln {(x+1)}] delim{|}{{{~}under{2}}over{3}}{}= =[- ln {(-x+5)}] delim{|}{{{~}under{0}}over{2}}{} + [ln {(x+1)}] delim{|}{{{~}under{2}}over{3}}{}=](/~spt/plugins/content/mathpublisher/img/math_975.5_95c0d38a5b35596e3b506116f7cc3fc5.png)
 . .
c) În cazul acestei limite, putem evident presupune că a>3. Atunci avem:

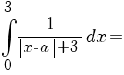

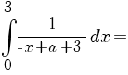
![=[- ln {(-x+a+3)}] delim{|}{{{~}under{0}}over{3}}{}= =[- ln {(-x+a+3)}] delim{|}{{{~}under{0}}over{3}}{}=](/~spt/plugins/content/mathpublisher/img/math_975.5_67687f0858e858c8c80874a8b9f82c36.png)
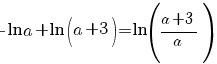 . .
Aşadar
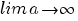
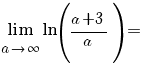
 . .
Ultima actualizare ( Luni, 04 Aprilie 2011 18:58 )
|




 .
.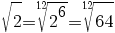 ;
; ;
; .
.
 .
.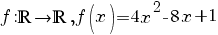 .
.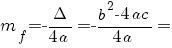
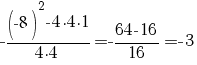 .
.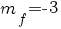 .
.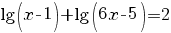 .
.
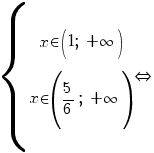
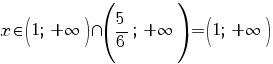 .
.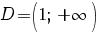 .
.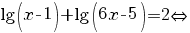


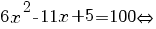
 .
.

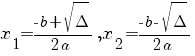
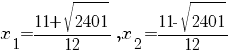

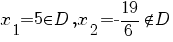 .
. .
. .
. de cazuri posibile (câte numere naturale de două cifre sunt). Prin urmare
de cazuri posibile (câte numere naturale de două cifre sunt). Prin urmare .
.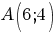 şi este perpendiculară pe dreapta
şi este perpendiculară pe dreapta  .
.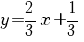 .
.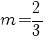 .
.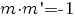
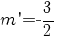 .
.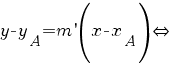
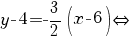

 .
. .
.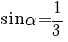 , să se calculeze
, să se calculeze  .
.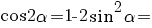
 .
.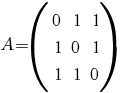 .
. .
.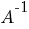 .
.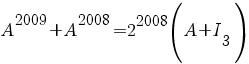 .
.
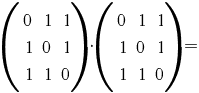
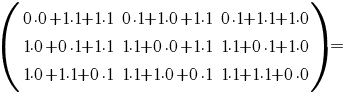
 .
.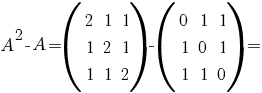
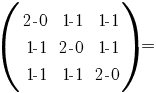

 , c.c.t.d.
, c.c.t.d.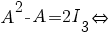
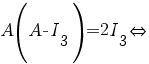
![A[1/2 (A-I_{3})]=I_{3} A[1/2 (A-I_{3})]=I_{3}](/~spt/plugins/content/mathpublisher/img/math_971_27c4faf4f1f52b95d5d5fb6f214911fd.png) .
.![[1/2 (A-I_{3})]A=I_{3} [1/2 (A-I_{3})]A=I_{3}](/~spt/plugins/content/mathpublisher/img/math_971_55596d423db5a5b0033831b5ef4f373e.png) .
.

 .
.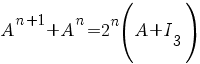 .
. .
.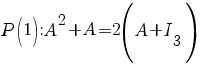 .
.

 .
.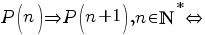
 .
. ;
;![A(A^{n+1}+A^{n})=A[2^{n}(A+I_{3})]{doubleleftright} A(A^{n+1}+A^{n})=A[2^{n}(A+I_{3})]{doubleleftright}](/~spt/plugins/content/mathpublisher/img/math_971_54649a707f75d0d35d8ef8e2aa679574.png)
![A(A^{n+1}+A^{n})=2^{n}[A(A+I_{3})]{doubleleftright} A(A^{n+1}+A^{n})=2^{n}[A(A+I_{3})]{doubleleftright}](/~spt/plugins/content/mathpublisher/img/math_971_c07e2037714a6c5dd6086d31f4826f00.png)
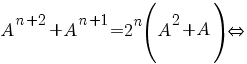 (dacă ne folosim de pasul I)
(dacă ne folosim de pasul I)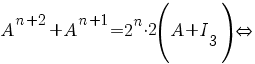
 .
.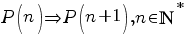 .
.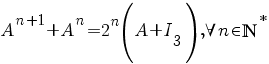 ,
,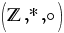 este un inel comutativ, unde
este un inel comutativ, unde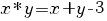
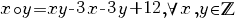 .
. ’ este 4.
’ este 4. astfel încât între inelele
astfel încât între inelele 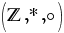 şi
şi  să existe un izomorfism de forma
să existe un izomorfism de forma  .
. ecuaţia
ecuaţia  .
. este element neutru al legii de compoziţie ‘
este element neutru al legii de compoziţie ‘

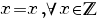 , (A).
, (A).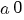 (adică f este bijectivă)
(adică f este bijectivă) .
.
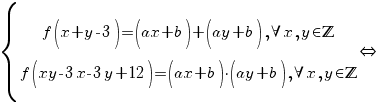
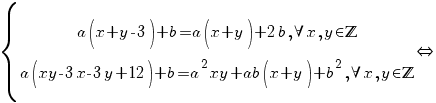
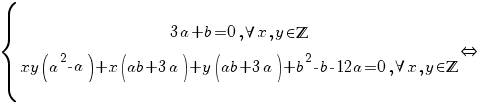
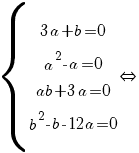
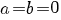 sau
sau  .
.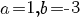 există un izomorfism între cele două inele, dat de legea
există un izomorfism între cele două inele, dat de legea 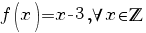 .
.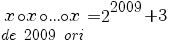


![[f(x)]^{2009}=2^{2009}+3-3{doubleleftright} [f(x)]^{2009}=2^{2009}+3-3{doubleleftright}](/~spt/plugins/content/mathpublisher/img/math_980_600d33f3401f270c4deb85807583cca2.png)
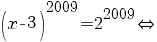
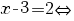
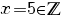 .
.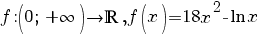 .
. pentru care
pentru care 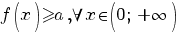 .
.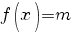 , unde m este un parametru real.
, unde m este un parametru real. şi
şi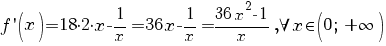 .
.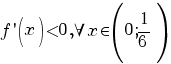 ;
;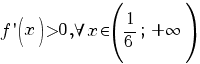 ;
;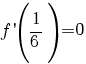 .
.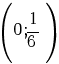 şi strict crescătoare pe intervalul
şi strict crescătoare pe intervalul 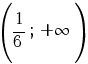 .
.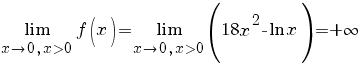 ;
;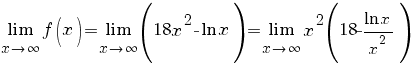 .
. .
.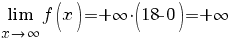 .
. .
.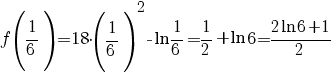
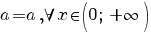 .
.![a in ({-infty}; ~ {2 ln {6}+1}/2] a in ({-infty}; ~ {2 ln {6}+1}/2]](/~spt/plugins/content/mathpublisher/img/math_992.5_b4c1998b2219348fdeb54da11a868a73.png) .
.
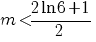 ecuaţia
ecuaţia 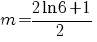 ecuaţia
ecuaţia  ;
; ecuaţia
ecuaţia 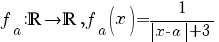 , unde
, unde 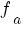 are primitive strict crescătoare pe
are primitive strict crescătoare pe 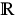 .
.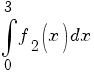 .
.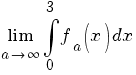 .
.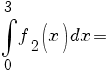
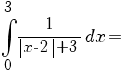
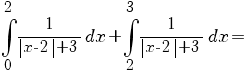


![=[- ln {(-x+5)}] delim{|}{{{~}under{0}}over{2}}{} + [ln {(x+1)}] delim{|}{{{~}under{2}}over{3}}{}= =[- ln {(-x+5)}] delim{|}{{{~}under{0}}over{2}}{} + [ln {(x+1)}] delim{|}{{{~}under{2}}over{3}}{}=](/~spt/plugins/content/mathpublisher/img/math_975.5_95c0d38a5b35596e3b506116f7cc3fc5.png)
 .
.
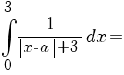

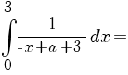
![=[- ln {(-x+a+3)}] delim{|}{{{~}under{0}}over{3}}{}= =[- ln {(-x+a+3)}] delim{|}{{{~}under{0}}over{3}}{}=](/~spt/plugins/content/mathpublisher/img/math_975.5_67687f0858e858c8c80874a8b9f82c36.png)
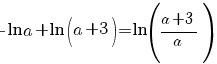 .
.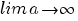
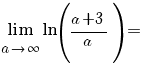
 .
.
